Ускоренное движение

Материал из Synset

Сказка о стволовых клетках <<	Оглавление	>> Равноускоренная система отсчета

$\textstyle \bullet$ Понятно, что в релятивистской теории равноускоренное движение, аналогичное классической механике, невозможно. Если скорость тела всё время увеличивается $\textstyle u(t)=a\cdot t$ , то она рано или поздно превысит фундаментальную скорость $\textstyle c$ . Это невозможно в силу энергетических ограничений, которые будут изучены в следующей главе. 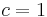Сейчас же мы рассмотрим один из вариантов ускоренного движения, при котором скорость постоянно увеличивается, оставаясь, тем не менее, все время меньше единицы ( $\textstyle c=1$ ).

Пусть для наглядности мимо неподвижного наблюдателя пролетает космический корабль, имеющий в данный момент времени скорость $\textstyle u=u(t)$ . Этот корабль плавно увеличивает свою скорость. Перейдём в систему отсчёта, связанную с ним (правый рисунок):

Так как за малое время $\textstyle dt'$ скорость корабля увеличивается незначительно, мы можем считать, что относительно своего предыдущего состояния она увеличилась на $\textstyle a\,dt'$ , где $\textstyle a$ — некоторая константа. По правилу сложения скоростей (2.2) новая скорость с точки зрения неподвижного наблюдателя равна:

$u(t+dt) = \frac{u(t)+a\, dt'}{1+u(t)\cdot a\,dt' }.$

Так как $\textstyle dt'$ мал, разложим знаменатель в ряд [ $\textstyle 1/(1+x)\approx 1-x$ ], и, сохраняя порядок малости, перемножим его с числителем:

$u(t+dt) \approx (u+a\, dt')(1-u\cdot a\,dt') \approx u + (1-u^2) \cdot a\,dt',$

где $\textstyle u=u(t)$ . Учитывая, что время по часам корабля $\textstyle dt'=dt\sqrt{1-u^2}$ идёт медленнее, и вводя производную скорости $\textstyle du/dt=[u(t+dt)-u(t)]/dt$ , получим:

$\frac{du}{dt} = a\cdot (1-u^2)^{3/2},\;\;\;\;\;\;\;\;или\;\;\;\;\;\;\;\;\frac{d}{dt} \left(\frac{u}{\sqrt{1-u^2}}\right) = a.$

(2.19)

Это дифференциальное уравнение описывает, как изменяется скорость некоторого объекта для неподвижного наблюдателя, если с "точки зрения" объекта, он пытается двигаться равноускоренно.

Выбрав начальное условие в виде $\textstyle u_0=u(0)$ и проинтегрировав это дифференциальное уравнение, получим:

$\frac{u(t)}{\sqrt{1-u^2(t)}}= \pi(t)=\pi_0+a\,t,\;\;\;\;\;\;\;где\;\;\;\pi_0=\frac{u_0}{\sqrt{1-u_0^2}}.$

(2.20)

Динамика величины $\textstyle \pi(t)=\pi_0+at$ совпадает с классической зависимостью увеличения скорости и она может быть сколь угодно большой. Однако релятивистская скорость $\textstyle u(t)$ всегда остаётся меньше единицы:

$u(t) = \frac{\pi_0+at}{\sqrt{1+(\pi_0+at)^2}}.$

(2.21)

Учитывая, что $\textstyle u(t)=dx/dt$ , после ещё одного интегрирования ( $\textstyle \lessdot$ H) с начальным условием $\textstyle x(0)=x_0$ можно получить траекторию движения:

$x(t) = x_0+\frac{1}{a} \left( \sqrt{1+(\pi_0+a\,t)^2} - \sqrt{1+\pi_0^2}\right).$

(2.22)

Напомним, что мы работаем в системе единиц, в которой 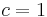$\textstyle c=1$ . Чтобы восстановить в формулах $\textstyle c$ , необходимо сделать замены $\textstyle t\mapsto ct$ , $\textstyle u\mapsto u/c$ и $\textstyle a\mapsto a/c^2$ , так как ускорение имеет размерность [ $\textstyle L/T^2$ ]. В этом случае и $\textstyle a\,t$ , и $\textstyle \pi_0$ будут делиться на $\textstyle c$ . В пределе $\textstyle c\to \infty$ , раскладывая в ряд по малым $\textstyle \pi_0$ и $\textstyle a\,t$ , мы получим хорошо известные классические выражения для движения равноускоренного объекта:

$u(t)\approx u_0+at+...,\;\;\;\;\;\;\;\;\;x(t)\approx x_0+u_0 t+ \frac{at^2}{2}+....$

Ниже приведены графики изменения скорости и координаты объекта, который ускоряется в течение единичного времени с единичным ускорением, а затем сразу начинает тормозить:

Верхние тонкие линии на каждом графике соответствуют классической равноускоренной динамике.

$\textstyle \bullet$ Как в равномерно двигающемся, так и в ускоренном корабле время замедляется. Рассмотрим этот эффект с позиции земного наблюдателя. Пусть корабль разгоняется в течении времени $\textstyle \tau_1$ , затем равномерно летит, и через время $\textstyle \tau_2$ начинает тормозить в течении времени $\textstyle \tau_1$ :

Вычислим собственное время путешествия, прошедшее на корабле. За малый интервал времени $\textstyle dt$ скорость корабля изменяется незначительно, и её можно рассматривать, как локально инерциальную систему отсчета. Поэтому время, прошедшее на двигающихся часах, связано со временем неподвижного наблюдателя следующим образом:

$dt'=\sqrt{1-u^2(t)}\,dt\;\;\;\;\;\;\;\;=>\;\;\;\;\;\;\;\;\;\;\;t'_2-t'_1 = \int\limits^{t_2}_{t_1} \sqrt{1-u^2(t)}\, dt.$

В результате этого интегрирования мы суммируем малые интервалы времени на Земле и на корабле. При этом предполагаем, что ускорение не влияет на ход времени. В следующем разделе мы подробнее остановимся на этом допущении.

Будем помечать, как и раньше, интервал времени у космонавта нулевым индексом. На первом этапе разгона корабля имеем:

$\tau_{01}=\int\limits^{\tau_1}_0 \sqrt{1-u^2(t)} \, dt = \int\limits^{\tau_1}_0 \frac{dt}{\sqrt{1+(at)^2}} = \frac{1}{a}\,\mathrm{ash}(a\,\tau_1),$

(2.23)

где $\textstyle \mathrm{ash}(x)$ — гиперболический арксинус, являющийся обратным к гиперболическому синусу ( $\textstyle \lessdot$ C):

$\mathrm{sh}(x)=\frac{e^x-e^{-x}}{2},\;\;\;\;\;\;\;\;\;\;\mathrm{ash}(x)=\ln (x+\sqrt{1+x^2})\approx x-\frac{x^3}{6}+....$

За время разгона $\textstyle \tau_1$ корабль достигает скорости [см. (2.21)]:

$u=\frac{a\tau_1}{\sqrt{1+(a\tau_1)^2}},$

и дальше двигается равномерно. Поэтому на втором этапе:

$\tau_{02} = \tau_2\sqrt{1-u^2} = \frac{\tau_2}{\sqrt{1+(a\tau_1)^2}}$

время замедляется наиболее сильно, так как скорость максимальна.

Финальный интервал времени при торможении равен

$\tau_{03}= \int\limits^{2\tau_1+\tau_2}_{\tau_1+\tau_2} \sqrt{1-u^2(t)} \, dt = \int\limits^{2\tau_1+\tau_2}_{\tau_1+\tau_2} \frac{dt}{\sqrt{1+(\pi_0+at)^2}} = \frac{1}{a}\,\mathrm{ash}(a\,\tau_1).$

Из соображений симметрии можно сразу взять результат разгона корабля. Складывая интервалы времени каждого этапа, окончательно получаем:

$\tau_0 = \frac{2}{a}\mathrm{ash}(a \tau_1) + \frac{\tau_2}{\sqrt{1+(a\tau_1)^2}}.$

Первое слагаемое меньше, чем $\textstyle \tau_1$ , а второе меньше, чем $\textstyle \tau_2$ . Их можно ( $\textstyle \lessdot$ H) разложить в ряд Тейлора:

$\tau_0 = 2\tau_1\cdot \Bigl[1-\frac{(a\tau_1)^2}{6}+...\Bigr] + \tau_2\cdot \Bigl[1-\frac{(a\tau_1)^2}{2}+...\Bigr].$

Время, прошедшее в неподвижной системе отсчета, равно $\textstyle 2\tau_1+\tau_2$ . Время путешествия по часам корабля $\textstyle \tau_0$ меньше, причём на ускоренных этапах оно замедлялось медленнее, чем на этапе равномерного движения.

Сделаем оценки времени полёта к звёздной системе Альфа-Центавра, удалённой от Земли на расстояние 4.3 световых лет. Световой год — это расстояние, которое свет проходит в течении года:

$1\;ly = (299792458\,m/s)\cdot(365.25\cdot 24\cdot 3600\;с) \approx 0.9461\cdot 10^{16}\;m = 0.307\;pk.$

Измеряя расстояние в световых годах, а время — в обычных годах, мы по-прежнему работаем в системе 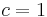$\textstyle c=1$ . В этой системе единичное ускорение $\textstyle 1\;ly/y^2= 9.5\;m/s^2$ близко к ускорению свободного падения на поверхности Земли. Пусть из соображений комфорта (искусственная гравитация) космический корабль двигается с ускорением $\textstyle a=1$ половину пути, а затем сразу начинает тормозить $(\textstyle \tau_2=0).$ С точки зрения Земли [см.(2.22)] половина пути к звезде $\textstyle x=4.3/2$ св. лет занимает время:

$x = \frac{1}{a}\left[\sqrt{1+(a\tau_1)^2}-1\right]\;\;\;\;\;\;=>\;\;\;\;\;\;\tau_1=\frac{1}{a}\sqrt{\left(1+ax\right)^2-1} = 3\;y.$

Соответственно, общее время полёта туда и обратно составит 12 лет. Собственное же время космонавта в момент возвращения будет равно $\textstyle 4\mathrm{ash}(a\tau_1)/a=7.3$ года, т.е. на 40% меньше. За 64 года собственного времени космонавт может "слетать" (вернувшись) к галактике Андромеды, удалённой на 2.5 млн. св. лет. На Земле пройдёт около 5 млн. лет. К сожалению, всё не так просто, и технологическая реалистичность подобных перелётов будет проанализирована в следующей главе.

Сказка о стволовых клетках <<	Оглавление	>> Равноускоренная система отсчета

Релятивистский мир - лекции по теории относительности, гравитации и космологии

Ускоренное движение

Материал из Synset

Просмотры

Личные инструменты

Навигация

почитай

Поиск

Инструменты