ETÄLUKIO - PITKÄ MATEMATIIKKA - Juuri- ja logaritmifunktiot (maa8)


	8:		Juuri- ja logaritmifunktiot

Logaritmifunktio

Logaritmi on eksponentti, johon tietty luku (kantaluku) on korotettava, jotta saadaan haluttu luku (numerus). Täsmällisesti määritellään:

$\displaystyle \mathsf{(a>0, a\neq 1, x>0})$

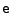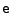Tietyn luvun logaritmin arvo riippuu siis kantaluvusta $\mathsf{a}$ . Yleisimmin käytetyt kantaluvut ovat $\mathsf{2}$ , $\mathsf{10}$ (Briggsin logaritmit $\mathsf{\log_{10} x= \lg x}$ ) ja $\mathsf{e}$ (luonnolliset logaritmit $\mathsf{\log_{e} x= \ln x}$ ). Laskimella voidaan tavallisesti laskea kantaluvuilla $\mathsf{10}$ ja $\mathsf{e}$ . Oheisissa kuvissa on logaritmifunktion $\mathsf{f(x)=\log_a x}$ kuvaaja piirretty kantaluvun arvoilla $\mathsf{a>1}$ ja $\mathsf{0<a<1}$ . Havaitaan, että kuvaajat muistuttavat paljolti vastaavia eksponenttifunktion kuvaajia.


a) logaritmifunktio a>1	b) logaritmifunktio 0 < a < 1

Myös logaritmifunktion ominaisuudet muistuttavat eksponenttifunktion ominaisuuksia. Funktio saa jokaisen reaaliarvon täsmälleen kerran ja on aidosti monotoninen. Kantaluvun $\mathsf{a>1}$ arvoilla funktio on aidosti kasvava ja arvoilla $\mathsf{0<a<1}$ aidosti vähenevä.

Logaritmien laskusäännöt

Kun $\mathsf{x>0}$ ja $\mathsf{y>0}$ ja $\mathsf{a>0,a\neq 1}$ , niin logaritmeille on voimassa seuraavat laskusäännöt:

$\displaystyle \mathsf{\log_a xy = \log_a x + \log_a y}$

$\displaystyle \mathsf{\log_a \frac{x}{y} = \log_a x - \log_a y}$

$\displaystyle \mathsf{\log_a x^r=r \cdot \log_a x}$

Nämä säännöt ovat johdettavissa vastaavista potenssien laskusäännöistä. Tutkitaan ensimmäistä sääntöä tarkemmin. Logaritmin määritelmän mukaisesti voidaan kirjoittaa

$\displaystyle \mathsf{x=a^{\log_a x}, \ \ \ \ \ y=a^{\log_a y}}$

Kerrotaan yhtälöt puolittain keskenään, jolloin saamme

$\displaystyle \mathsf{xy=a^{\log_a x + \log_a y}}$

Logaritmin määritelmän mukaan tästä saadaan

$\displaystyle \mathsf{\log_a xy = \log_a x + \log_a y}$

Voit tutkia kaksi muuta sääntöä vastaavalla tavalla harjoituksena.

Joskus on tarpeen siirtyä logaritmijärjestelmästä toiseen eli vaihtaa käytettävää kantalukua. Tämä tapahtuu seuraavalla säännöllä

$\displaystyle \mathsf{\log_a x = \frac{\log_b x}{\log_b a}}$

Logaritmifunktion piirtäminen

Logaritmifunktion piirtäminen onnistuu seuraavan ohjeen avulla.

Logaritmifunktion piirtäminen

1. Tutki mikä on funktion määrittelyjoukko eli milloin numerus on positiivinen.

2. Etsi funktion kuvaajan pystysuora asymptootti. Asymptoottina on suora $\mathsf{x=c}$ , missä $\mathsf{c}$ on määrittelyjoukon ala- tai yläraja (toinen rajoista on usein $\mathsf{\pm \infty}$ ).

3. Selvitä x-akselin ja kuvaajan leikkauskohta merkitsemällä funktion arvoksi $\mathsf{0}$ ja ratkaisemalla vastaava yhtälö.

4. Selvitä y-akselin leikkauskohta sijoittamalla $\mathsf{x}$ :n arvoksi $\mathsf{0}$ . (Leikkauskohtaa ei välttämättä ole).

5. Laske joitakin funktion arvoja kohdassa 3 ratkaistun leikkauspisteen läheisyydessä.

6. Piirrä kuvaaja pisteiden ja asymptootin avulla.

Huom: Kohdan 3 yhtälö on usein muotoa

$\displaystyle \mathsf{\log_a L = 0}$

missä $\mathsf{L}$ on jokin $\mathsf{x}$ :n lauseke. Koska kaikkien kantalukujen potenssi saa arvon 1 vain eksponentin ollessa 0, voidaan yhtälö ratkaista seuraavasti

$\displaystyle \mathsf{2^{\log_a L} = 2^0}$

$\displaystyle \mathsf{L = 0}$

Logaritmiyhtälöiden ratkaisemista käsitellään tarkemmin seuraavassa osiossa.

Alla oleva kuvaaja havainnollistaa logaritmifunktion $\mathsf{f(x)=\log_a x}$ riippuvuutta kantaluvusta. Voit muuttaa kantaluvun arvoa hiirtä napauttamalla.